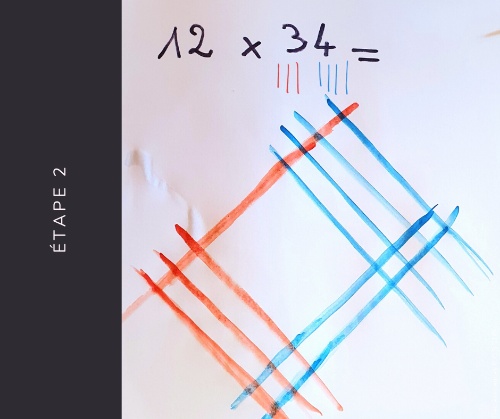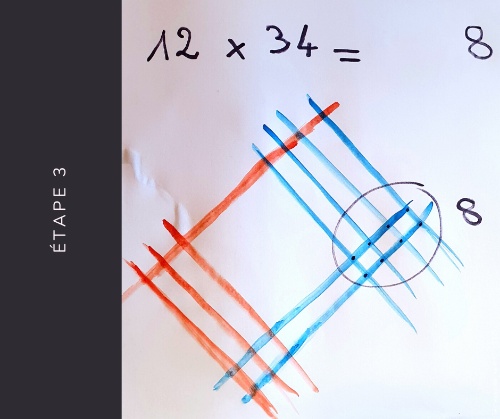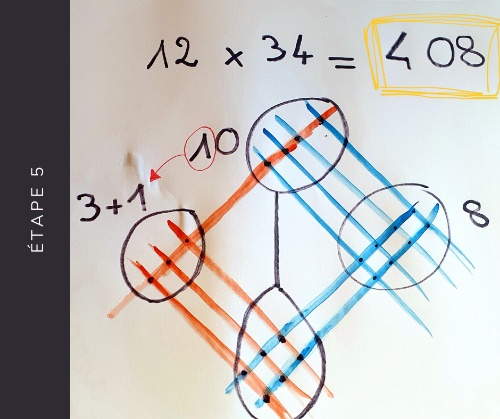Recette
Mme Sciences chez les Mayas
… avec mme Sciences !
Matériel
Durée de l’expérience
À partir de 10 ans
1
On va calculer la multiplication 12 x 34.
Avec le stylo rouge on dessine 1 trait en diagonale qui représente la dizaine de 12. On prend ensuite le stylo bleu et, un peu plus bas, on dessine 2 traits qui représentent les unités.
2
On passe maintenant au nombre 34. Il faut reprendre le stylo rouge et dessiner 3 traits pour les 3 dizaines. Puis, de façon à faire un carré, on dessine 4 traits bleus pour les unités. (comme sur la photo)
3
Trouvons le résultat de cette multiplication: on entoure les intersections des traits bleus, puis on les compte. Elles représentent les unités, ici on en a 8.
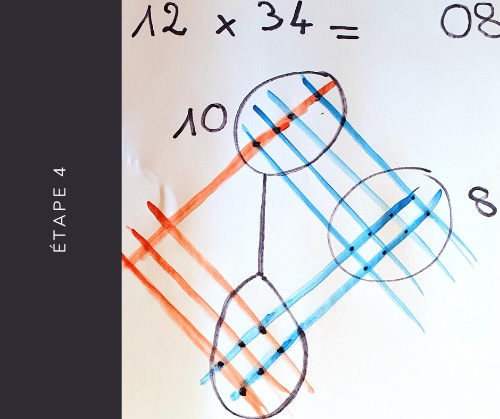
4
Pour les dizaines, on fait la même chose là où le bleu croise le rouge. Dans notre cas, on compte 10 intersections, cela veut dire qu’on a 1 centaine, qu’on retient, et 0 dizaine.
5
Pour finir on compte les intersections entre les traits rouges. Cela représente les centaines. On en compte ici 3 auxquelles on ajoute c’elle qu’on a retenue.
On a donc 4 centaines, 0 dizaine et 8 unités, ce qui donne 408.
Explications simples :
Cette méthode pour poser les multiplications est enseignée au Japon. Cependant, elle est bien plus vieille puisque les Mayas l’utilisaient déjà. C’est une méthode visuelle qui est pourtant très proche de la nôtre. En effet, les deux sont basées sur la décomposition des nombres en unités, dizaines, centaines (…). La méthode japonaise est plus rapide que la nôtre pour les petites multiplications, mais devient plus compliquée quand on augmente la taille des nombres.
Explications mathématiques : niveau collège/lycée
Comme dit plus haut, on se base sur la décomposition. Dans notre cas, on a 12 x 34 que l’on peut décomposer de la manière suivante :
(10 + 2) x (30 + 4)
Comme pour les traits, on a les dizaines en rouge et les unités en bleu. On peut maintenant procéder à la multiplication en utilisant la distributivité. Ce qui donne :
(10 x 30) + (10 x 4 + 30 x 2) + (2 x 4)
= 300 + 100 + 8
On retombe alors sur les 3 sections qu’on avait dessinées. Une section bleue avec 8 unités, une bleue et rouge avec 10 dizaines (1 centaine retenue et 0 dizaine) et enfin une rouge avec les 3 centaines auxquelles on ajoute la centaine retenue. On obtient donc 408.
Pour aller plus loin :
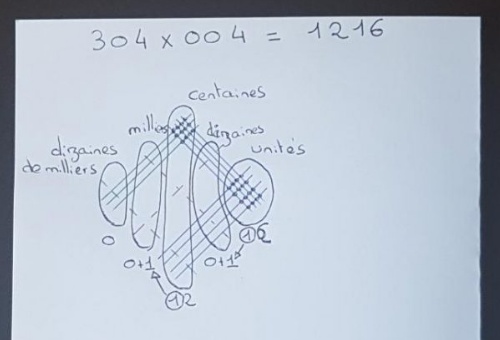
Si l’on veut faire des multiplications avec des nombres qui contiennent des 0. On procédera de la même manière mais en indiquant le 0 par un trait pointillé. On ne comptera pas les intersections avec un tel trait mais cela nous permet de respecter les zones. De plus, si on a un nombre composé de 3 chiffres et un avec un seul, on complètera avec des 0. Voici en exemple 304 x 004 :